String Vibrations and Overtones
Understanding overtone and harmonic nodes along a vibrating string
The picture below (Fig. 1) is a model of how a string vibrates. At half the length we have the same note but an octave higher (the 12th fret), and this is called the second harmonic on the open string. At those nodes, we can find the harmonics of the string, also called overtones.
For example, if the length of a string is 64 cm, the 2nd harmonic would be at 32 cm, the 3rd at 21.33 cm, and so on.
Fig. 1 – Model of string vibration with harmonic nodes
The easiest way to understand harmonics is to use flageolets. At the seventh fret we have the third harmonic (one-third of the open string's length). The same harmonic can also be reproduced higher up the neck at the 19th fret. At the fifth fret we find the fourth harmonic.
Harmonics follow a factor-of-two pattern, as you can see in Fig. 1. So what does this mean in terms of frequency?
Let’s use the A string as an example
Spectrum analysis of a guitar string at A. To my ears, the pitch of the open A string is A3, which is 220 Hz.
Oddly enough, when looking at the Fast Fourier Transform (FFT) analysis in Fig 2, the strongest low-frequency component appears at 110 Hz, which corresponds to A2—one octave below. You can check it out in Analyze Instrument Frequencies.
This doesn't mean the string is producing the wrong pitch. Instead, it reveals that the physical vibration of the string includes a strong first overtone (or subharmonic) at 110 Hz. This is common in complex acoustic sounds, where overtones can be stronger than the perceived fundamental.
How can this be?
Where is the fundamental?
Three possible explanations
1. The string’s vibration includes a strong subharmonic or first overtone
The string may be vibrating in a way that includes both A2 (110 Hz) and A3 (220 Hz), with A2 showing up more prominently in the spectrum.
This can happen especially when the pickup or microphone captures low-frequency energy well, or if you're plucking the string in a way that excites lower modes. Lower frequencies also tend to carry more energy, making them more visible in a spectrum analysis.
2. The FFT shows actual physical vibrations, not necessarily perceived pitch
The FFT simply reports what frequencies are physically present, and sometimes the actual fundamental (220 Hz) isn’t always the strongest component in the spectrum.
In some recordings, the second harmonic (220 Hz) might dominate, while the true lowest mode (110 Hz) may sneak in underneath—even if it’s not what your ear focuses on.
3. Perceptual pitch ≠ spectral fundamental
Human ears tend to perceive the pitch as 220 Hz, even if the lowest frequency component is 110 Hz.
This phenomenon is part of how our brains construct pitch based on harmonic relationships, not just the lowest frequency present.
In summary
Our perception of pitch isn't based solely on the lowest frequency in a sound. Instead, our brains use the pattern of harmonics—multiples of a fundamental—to determine what pitch we "hear." This is known as the "missing fundamental phenomenon".
Even if the fundamental frequency (e.g. 220 Hz) is absent or very weak, the brain recognizes that the overtones (440 Hz, 660 Hz, etc.) fit the pattern of a harmonic series starting at 220 Hz. It fills in the missing piece and assigns the pitch accordingly.
Frequency spectrum of the open A string
Fig 2
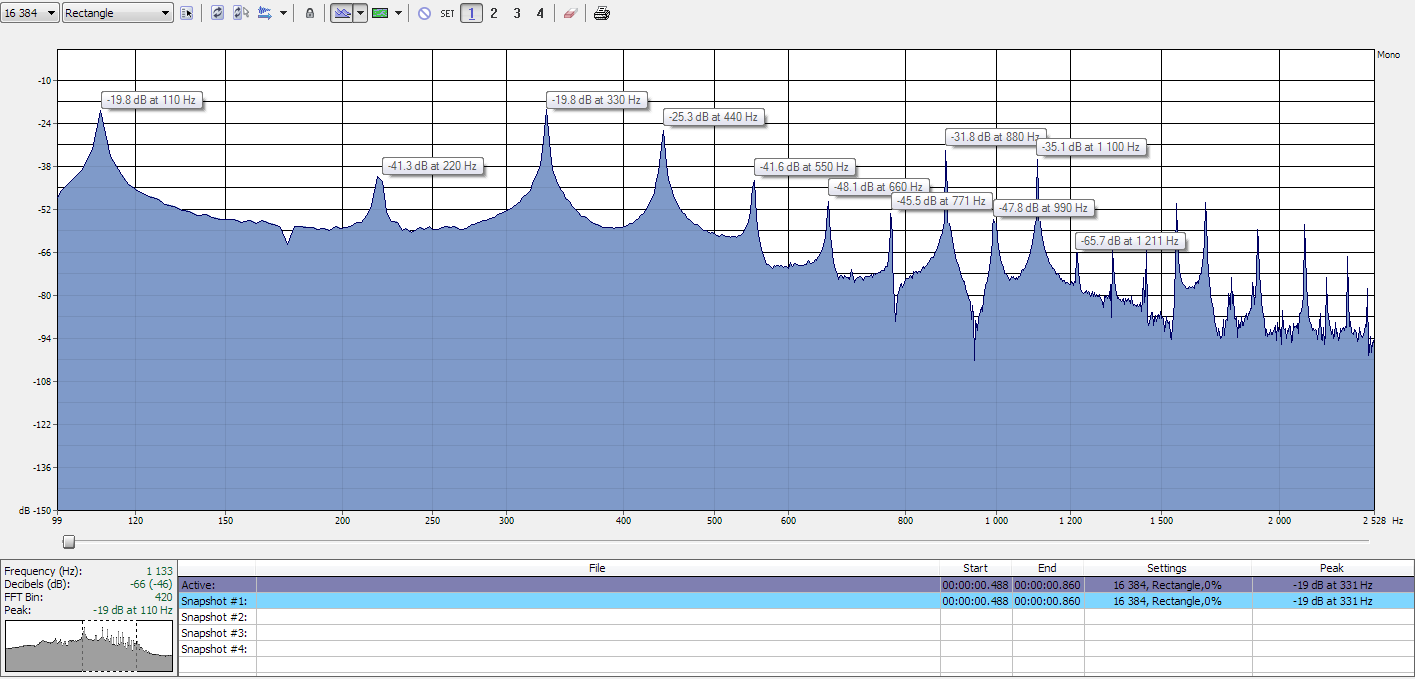
What we see in Fig. 2
The graph in Fig. 2 shows a frequency spectrum of the A string using FFT analysis. Each peak represents a harmonic (or overtone) present in the sound. The first peak appears at 110 Hz—A2—even though the perceived pitch is A3 (220 Hz). This reflects the actual physical vibration modes of the string, not necessarily the pitch we hear.
As we move along the x-axis, the peaks appear at regular intervals: 220 Hz, 330 Hz, 440 Hz, and so on. These are the harmonics of the string, and their spacing follows a harmonic series based on the fundamental frequency of 110 Hz. The height of each peak shows the relative strength (amplitude) of each harmonic in the sound. In the FFT graph, you can see prominent peaks at:
- 110 Hz (1st harmonic, possibly the strongest peak)
- 220 Hz (2nd harmonic / perceived pitch)
- 330 Hz (3rd harmonic)
- 440 Hz (4th harmonic)
- ...
This series outlines the integer multiples of the fundamental frequency—each representing a harmonic or overtone that contributes to the sound’s timbre.
Using the model in Fig. 1 and the overtone peaks in the FFT analysis (Fig. 2), we can see that:
- 110 + 110 = 220 Hz
- 110 + 110 + 110 = 320 Hz
- 110 + 110 + 110 + 110 = 440 Hz
Written as a formula:
Nth Harmonic Frequency = Fundamental Frequency × N
Or for example:
- 110 Hz = 110 × 1st harmonic
- 220 Hz = 110 × 2nd harmonic
- 330 Hz = 110 × 3rd harmonic
- 440 Hz = 110 × 4th harmonic
- ...and so on
Overtones (harmonics) of the A string:
- 110 Hz
- 220 Hz
- 330 Hz
- 440 Hz
- 550 Hz
- 660 Hz
- 770 Hz
- 880 Hz
- 990 Hz
- 1100 Hz
- 1210 Hz
- ...and so on
As we can see in the spectrogram there are a lot of overtones in a vibrating string.
Check out Frequency Analysis of Different Instruments, a real time FFT (Fast Fourier Transform) JavaScript analyser where you can see the frequency response of different instruments.
Related: What Happens in Plugins?
If you're interested in how harmonic content is affected by audio processing, take a look at Plugin Harmonics. There you can explore how plugins add even and odd harmonics to a signal, and analyze them using a frequency analyzer.
|•|eamusic
